Graph Theory-The shortest path

发表于 | 分类于 | | 阅读次数:

　　$Bellman-Ford、SPFA、Dijkstra$这些单源最短路算法自己一直都在用，但有时候只是需要的时候拿出来当板子敲上去，没有什么深刻的理解，今天花了一下午把这些算法的原理和一些细节基本搞通了，总结一下。

　　$PS：Floyd-Warshall$多源最短路算法受限于自己对DP的理解，还没有完全搞明白= =，之后再来填坑。
　　Bellman-Ford代码、Dijkstra理解和代码部分参考自《挑战程序设计竞赛》。

限制和复杂度

　　$Bellman-Ford$：不含负圈（可判断出）。运行时间：$O(|V|*|E|)$。
　　$SPFA$：不含负圈（可判断出）。运行时间：$O(k*|E|)$，一般情况下$(k <<|V|)$，可以认为近似线性。
　　$Dijkstra$：不含负权边。运行时间：$O(|E|*|log|V|)$（优先队列实现）

Bellman-Ford

　　$Bellman-Ford$算法思想是更新所有的边，每条边都更新$|V|-1$次，由于多余的更新操作是无害的，所有算法可以求得最短路，但同时不可避免的有复杂度冗余的问题。
　　先说一下为什么是更新$|V|-1$次：
　　首先每一个节点$v$都有一条相对于起点$s$的最短路，因为最短路是简单路径不包含环（如果是负环，最短路不存在；如果是正环，去掉后变短；如果是零环，去掉后不变），所以节点总数为$|V|$的情况下最长的那条最短路的长度不会超过$|V|-1$，又因为每更新一次都必然会确定最短路径上的一条线段，所以最多只需要更新$|V|-1$次，反之，如果更新次数超过$|V|-1$次则说明图中有负环最短路不存在，可以利用这一点来判断图中是否有负环。
关于“每更新一次都必然会确定最短路径上的一条线段“的进一步解释：

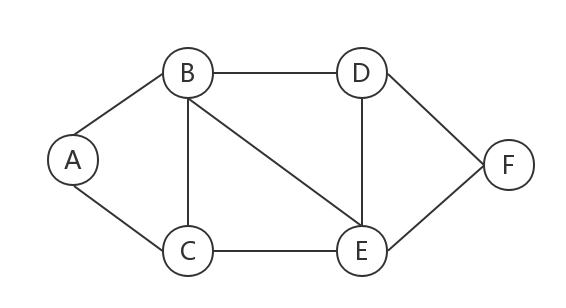
graph

　　以上图为例，假设上图中的最长的一条最短路为$A->F$的最短路

path

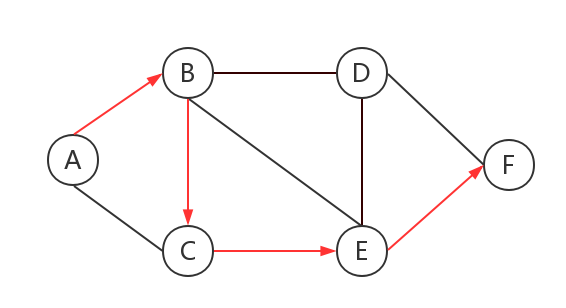
　　从原点$A$开始出发，每次进行所有边的更新，第一次更新结束后$A->B$的最短路确定，第二次更新结束后$A->C$的最短路确定，以此类推四次后这条最长的最短路确定。因为这条最短路是最长的，所以在它确定时其它较短的最短路也肯定已经确定。所以在至多$|V|-1$次更新后$Bellman-Ford$算法可以找到任意一条最短路。

$Bellman-Ford$代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
//从顶点from指向顶点to的权值为cost的边
struct edge{
    int from;
    int to;
    int cost;
};

edge es[MAX_E]; //边

int d[MAX_V];   //最短距离
int V, E;       //顶点数和边数

//求解从顶点s出发到所有点的最短距离
void short_path(int s){
    fill(d, d + V, INF);
    d[s] = 0;
    while(true){
        bool update = false;
        for(int i = 0; i < E; i++){
            edge e = es[i];
            if(d[e.from] != INF && d[e.to] > d[e.from] + e.cost){
                d[e.to] = d[e.from] + e.cost;
                update = true;
            }
        }
        if(!update) break;
    }
}

SPFA

　　$SPFA$算法可以用一句话概括：”只有被更新了的节点才有资格更新其它节点“。因为如果一个节点自身没有被更新的话，那用它更新与它相邻的其它节点也不会产生新的结果。它用队列来维护那些被更新了节点。值得注意的是虽然一般情况来说$SPFA$的复杂度接近线性，但它不稳定，可以构造出特殊的图使得SPFA的复杂度变为和$Bellman-Ford$一样。

$SPFA$代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
struct edge{
    int to;
    int cost;
};

vector<edge> G[MAX_V];  //邻接表

int d[MAX_V];
bool vis[MAX_V];

void spfa(int s) 
{
    queue<int> q;
    memset(vis, 0, sizeof(vis));
    fill(d, d + V, INF);
    d[s] = 0;
    q.push(s);
    vis[s] = true;
    while (!q.empty()) 
    {
        int v = q.front(); 
        q.pop(); 
        vis[v] = false;
        for(int i = 0; i < G[v].size(); i++)
        {
            edge e = G[v][i];
            if (d[e.to] > d[v] + e.cost) 
            {
                d[e.to] = d[v] + e.cost;
                if (!vis[e.to])
                {
                    vis[e.to] = true;
                    q.push(e.to);
                }
            }
        }
    }
}

Dijkstra

　　考虑没有负边的情况。在$Bellman-Ford$算法中，如果$d[i]$还不是最短距离的话，那么即使进行$d[j]=d[i]+l(i, j)$的更新，$d[j]$也不会变成最短距离。而且，即使$d[i]$没有变化，每一次循环也要检查一遍从$i$出发的所有边。这显然是很浪费时间的。因此可以对算法做如下修改：

  1. 找到最短距离已经确定的顶点，从它出发更新相邻的顶点的最短距离。
  2. 此后不需要再关心$1$中的”最短距离已经确定的顶点“。

　　在$1$和$2$中提到的”最短距离已经确定的顶点“要怎么得到是问题的关键。在最开始时，只有起点的最短距离是确定的。而在尚未使用过的顶点中，距离$d[i]$最小的顶点就是已经确定的顶点。这是因为由于不存在负边，所以$d[i]$不会在之后的更新中变小。

$Dijkstra$代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
struct edge{
    int to;
    int cost;
};
typedef pair<int, int> P;

int V;
vector<edge> G[MAX_V];
int d[MAX_V];

void dijkstra(int s){
    priority_queue<P, vector<P>, greater<P> > que;
    fill(d, d + V, INF);
    d[s] = 0;
    que.push(P(0, s));

    while(!que.empty()){
        P p = que.top();
        que.pop();
        int v = p.second;
        if(d[v] < p.first) continue;    //v点的距离已被更新为更小的值，队列中的值丢弃
        for(int i = 0; i < G[v].size(); i++){
            edge e = G[v][i];
            if(d[e.to] > d[v] + e.cost){
                d[e.to] = d[v] + e.cost;
                que.push(P(d[e.to], e.to));
            }
        }
    }
}