Uva839-二叉树的递归处理

发表于 | 分类于 ， | | 阅读次数:

输入一个树状天平，根据力矩相等原则判断是否平衡。即判断是否满足$W_lD_l=W_rD_r$。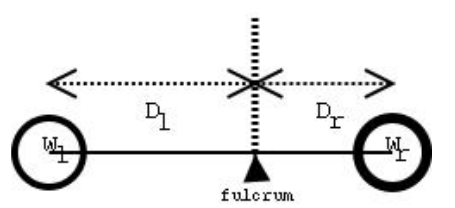
example

链接

Uva839-Not so Mobile

题目描述

题目输入采用递归（先序）方式：每个天平的格式为$W_l$，$D_l$，$W_r$，$D_r$，当$W_l$或$W_r$为$0$时，表示该“砝码”实际是一个子天平，接下来会进一步描述这个子天平。当$W_l=W_r=0$时，会先描述左子天平，然后是右子天平。

题解

因为题目的输入就采取了递归方式定义，所以编写一个递归过程读取输入同时进行处理比较合适。在递归的过程中判断子天平是否满足平衡并自下向上不断的更新$W$为$0$的节点（更新为其左子砝码重量$W_l$和右子砝码重量$W_r$之和）。可以定义一个标志变量来标明整个过程是否一直都满足平衡条件。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
/*
 *
 * Author : Aincrad
 *
 * Date : Sat 22 Sep 22:02:34 CST 2018
 *
 */
 
#include <bits/stdc++.h>

using namespace std;

int t;
bool f;

int solve(){
    int w1, d1, w2, d2;
    cin >> w1 >> d1 >> w2 >> d2;
    if(!w1) w1 = solve();
    if(!w2) w2 = solve();
    if(w1 * d1 != w2 * d2) f = false;
    return w1 + w2;
}

int main(){
    //ios::sync_with_stdio(false);
    //cin.tie(0);
    //cout.tie(0);
    #ifndef ONLINE_JUDGE
        freopen("in.txt", "r", stdin);
    #endif
    
    cin >> t;
    while(t--){
        f = true;
        solve();
        if(f) cout << "YES" << endl;
        else cout << "NO" << endl;
        if(t) cout << endl;
    }
    
    return 0;
}