八皇后问题

发表于 | 分类于 | | 阅读次数:

八皇后问题，即在$8 \times 8$的棋盘上放置8个皇后，使得它们互不攻击（皇后的攻击范围为同行同列和同对角线）。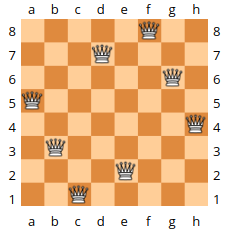
queen

参考

刘汝佳《算法竞赛入门经典》（第2版）

解法

比较容易想到的一个思路是把这个问题转换为“从64个格子中选8个格子”的问题。但是这一共有$C^8_{64} = 4.426 \times 10^9$种情况。我们可以考虑先排除一些明显不成立的情况，减少枚举量。首先八个皇后肯定是位于不同行不同列的，所以逐行放置可以把这个问题看做一个求$0-7$列的全排列问题。这样的话总的情况数为$8! = 40302$种，同时用回溯法进行剪枝操作，可以在1秒内完成检索。
$(i，C[i])$和$(j，C[j])$分别表示两个皇后坐标，它们位于同一对角线上的条件：
i - C[i] == j - C[j] || i + C[i] == j + C[j]

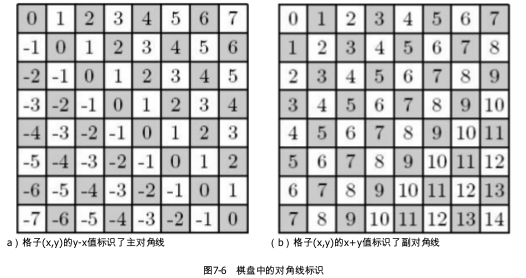
diagonal

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include <bits/stdc++.h>

using namespace std;

const int N = 8;
bool vis[3][100]; //record visited columns and  diagonals
int c[100]; //represent columns
int cnt;

void dfs(int n){
    if(n == N){
        cnt++;
        for(int i = 0; i < N; i++){
            cout << c[i] << " ";
        }
        cout << endl;
        return;
    }
    for(int i = 0; i < N; i++){
        // n - i　could be negative number, so we plus N.
        if(!vis[0][i] && !vis[1][n + i] && !vis[2][n - i + N]){
            c[n] = i;
            vis[0][i] = vis[1][n + c[n]] = vis[2][n - c[n] + N] = 1;
            dfs(n + 1);
            vis[0][i] = vis[1][n + c[n]] = vis[2][n - c[n] + N] = 0;
        }
    }
}

int main(){
    memset(vis, 0, sizeof(vis));
    memset(c, -1, sizeof(c));
    cnt = 0;
    dfs(0);
    cout << endl;
    cout << "total number: " << cnt << endl;
    return 0;
}