八数码问题,最开始是在人工智能基础课上学的,然而我已无力吐槽这门课了,现在我才回想起来原来她当时所讲的open表其实就是栈和队列。而当时那些手算看起来很简单的搜索算法,实际写起来还是会有很多坑的,如果现在再重新学这门课我应该会有很多新的思考和认识吧。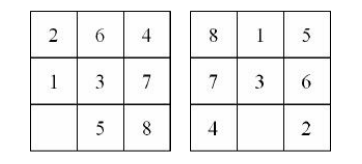
八数码问题
编号为$1-8$的八个正方形滑块被摆成3行3列,其中有一个格子留空。每次可以把与空格相邻的滑块移到空格中,它原来的位置就成了新的空格。给定初始局面和目标局面,计算最少的移动步数。
因为是计算最少移动步数,所以用BFS来搜索比较合适。但是和一般的图搜索不太一样,这里没有显式的结点。可以想到把每一个“状态”看做图的一个结点,然后根据合法的移动方式去扩展其它结点,直到到达目标状态。
还有一个问题是如何标记已经访问过的状态,以避免对同一个结点做多次访问。在显式的图搜索里我们一般会开一个vis数组来标记,但是这里如果要用vis数组的话,要开到九维,$9^9$,这对空间的消耗太大了。于是我们可以考虑用之前提到的哈希,每一个状态对应一个整型数,一共的状态数是$9! = 362880$种。这样我们用一个vis数组就可以表示出来了。
下面的代码是用STL里的set代替vis数组实现判断状态是否已访问过
代码
1 | /* |
打印路径版代码
1 |
|