Uva11212-Editing a Book-IDA*

发表于 | 分类于 ， | | 阅读次数:

有$n（1 < n < 10）$个段落初始按一定顺序排列，要求通过“剪切”和“粘贴”操作把这n个段落调整为按编号1，2，…，n顺序排列。其中每次可以同时剪几个连续的段落，求最少的操作步数。

链接

Uva11212-Editing a Book

题解

如果采用BFS进行状态搜索，总的状态数为$9! = 362880$，这个状态数量不是很大，但是每个状态的后继转移情况很多（可以剪切任意一个区间粘贴在剪切后的序列的任意一个位置处），所以可能会超时。
采用IDA*求解，可以发现$n <= 9$ 时最多只需要8步，因为深度上限为8。接下来考虑剪切时的启发函数，统计序列中后继不正确的数字个数h，可以证明每次剪切时h最多减少3，因此当h / 3 > maxd - d，即3d + h > 3maxd时可以剪枝，其中d为当前深度，maxd为深度限制。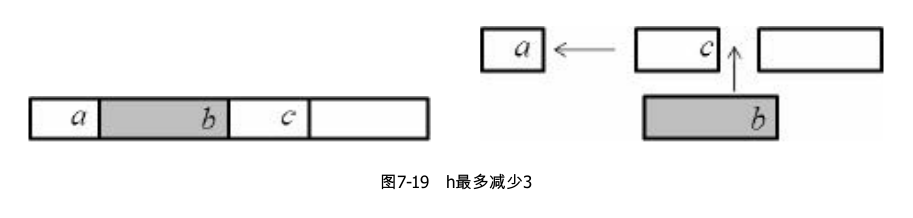
prune

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
/*
 *
 * Author : Aincrad
 *
 * Date : Fri 11 Jan 21:47:39 CST 2019
 *
 */

#include <bits/stdc++.h>

using namespace std;

const int maxn = 10;
int n;
int d[maxn];
int maxd;

bool judge(){
    for(int i = 0; i < n - 1; i++){
        if(d[i] > d[i + 1]) return false;
    }
    return true;
}

int h(){
    int cnt = 0;
    for(int i = 0; i < n - 1; i++){
        if(d[i] != d[i + 1] - 1) cnt++;
    }
    if(d[n - 1] - d[0] != n - 1) cnt++;
    return cnt;
}

bool dfs(int dep, int maxd){
    if(3 * dep + h() > 3 * maxd) return false;
    if(dep >= maxd){
        if(judge()) return true;
        else return false;
    }
    int tmp[10], oldd[10];
    memcpy(oldd, d, sizeof(d));
    for(int i = 0; i < n; i++){
        for(int j = i; j < n; j++){
            
            //cut
            int cnt = 0;
            for(int k = 0; k < n; k++){
                if(k < i || k > j) tmp[cnt++] = d[k];
            }

            //find a position to paste before it
            int cnt2;
            for(int k = 0; k <= cnt; k++){
                cnt2 = 0;
                for(int p = 0; p < k; p++) d[cnt2++] = tmp[p];
                for(int p = i; p <= j; p++) d[cnt2++] = oldd[p];
                for(int p = k; p < cnt; p++) d[cnt2++] = tmp[p];
                if(dfs(dep + 1, maxd)) return true;
                memcpy(d, oldd, sizeof(d));
            }
        }
    }
    return false;
}

int main(){
    #ifndef ONLINE_JUDGE
        freopen("in.txt", "r", stdin);
    #endif

    int kase = 0;
    while(cin >> n){
        if(n == 0) break;
        for(int i = 0; i < n; i++){
            cin >> d[i];
        }
        for(maxd = 0; maxd < 10; maxd++){
            if(dfs(0, maxd)) break;
        }
        cout << "Case " << ++kase << ": " << maxd << endl;
    }
    return 0;
}