Uva1602-Lattice Animals-搜索+仿射变换技巧

给定$n，w，h$，求在$n \times n$的网格中，最多能放入几种宽和高不超过$w和h$的连通块。其中一个连通块经过平移、旋转和翻转得到的连通块不属于新的连通块。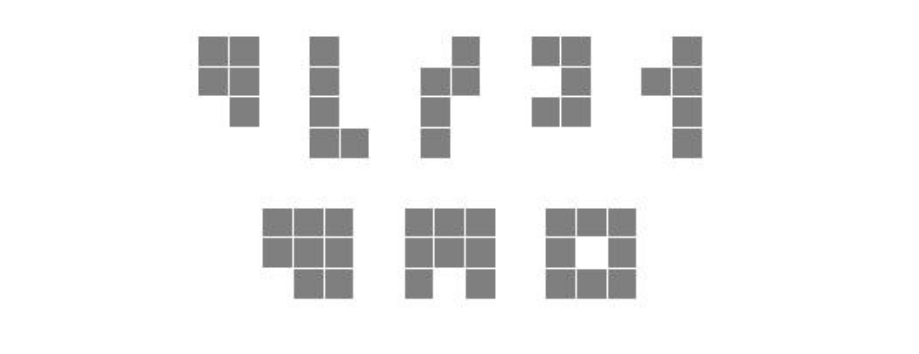

链接

题目链接：Uva1602-Lattice Animals
参考链接：XDU_Skyline’s Blog，Rujia Liu’s Github Repository

题解

分为两部分，一部分为搜索，另一部分为判重。
搜索可以采用BFS也可以采用DFS。示例代码里采用了BFS。
判重部分，因为一个连通块经过平移、旋转和翻转后得到的连通块不属于新的连通块，所以在判断一个连通块是否重复时首先要对其每一种可能的形态进行判断。
对于平移操作，我们考虑将连通块进行标准化normalize，即统计连通块的x方向和y方向的最小值minX和minY，然后将连通块中的每一个单元格都减去矢量(minX，minY)得到标准化后的连通块。
对于旋转操作，假设一个单元格的坐标为(x，y),表示逆时针旋转90°的旋转矩阵为
$$
\begin{bmatrix}
0 & -1 \\
1 & 0
\end{bmatrix}
$$
所以该单元格逆时针旋转90°之后的坐标为(-y, x)。对连通块中的每一个单元格都执行此操作就得到了旋转后的连通块。旋转之后的连通块还要进行一次normalize操作再判重。
对于翻转操作，可以沿x轴翻转也可以沿y轴翻转。其对应的坐标变换是(x，y)->(-x，y)。(以沿y轴翻转为例)。翻转之后还要进行一圈的旋转判重，事实上沿x轴进行翻转后再旋转180°就可以得到沿y轴翻转后的图形，所以不需要再分开讨论这两种不同的翻转情况。同样翻转之后的连通块也要进行normalize操作后再判重。

以上是思路部分，关于具体的实现，搜索部分采用BFS，判重部分利用STL中的set判重。单元格通过一个结构体存储x和y坐标来表示，联通块通过set存储其各个单元格来表示。连通块之所以用set表示，而不是vector，是因为set会自动排序，这样就避免了因插入顺序不同导致的判重失败问题。

代码

/*
 *
 * Author : Aincrad
 *
 * Date : Mon 11 Feb 22:03:44 CST 2019
 *
 */

#include <bits/stdc++.h>

using namespace std;

const int maxn = 10;
const int inf = 100;
int dx[] = {0, 1, 0, -1};
int dy[] = {1, 0, -1, 0};
struct Cell{
    int x, y;
    Cell(int x = 0, int y = 0):x(x), y(y){}
    bool operator <(const Cell& c) const{
        if(this->x == c.x) return this->y < c.y;
        else return this->x < c.x;
    }
};
typedef set<Cell> Polyomino;
set<Polyomino> Poly[maxn + 1];

Polyomino normalize(Polyomino p){
    Polyomino p0;
    int minx, miny;
    minx = miny = inf;

    for(Polyomino::iterator t = p.begin(); t != p.end(); t++){
        minx = min(minx, t->x);
        miny = min(miny, t->y);
    }
    for(Polyomino::iterator t = p.begin(); t != p.end(); t++){
        p0.insert(Cell(t->x - minx, t->y - miny));
    }
    return p0;
}

Polyomino rotate(Polyomino p){
    Polyomino p0;
    for(Polyomino::iterator t = p.begin(); t != p.end(); t++){
        p0.insert(Cell(-t->y, t->x));
    }
    return normalize(p0);
}

Polyomino flip(Polyomino p){
    Polyomino p0;
    for(Polyomino::iterator t = p.begin(); t != p.end(); t++){
        p0.insert(Cell(-t->x, t->y));
    }
    return normalize(p0);
}

void check(Polyomino p, Cell c, int n){
    p.insert(c);

    p = normalize(p);
    for(int i = 0; i < 4; i++){
        if(Poly[n].count(p) != 0) return;
        p = rotate(p);
    }

    p = flip(p);
    for(int i = 0; i < 4; i++){
        if(Poly[n].count(p) != 0) return;
        p = rotate(p);
    }

    Poly[n].insert(p);
}

void search(){
    Polyomino p1;
    p1.insert(Cell(0, 0));
    Poly[1].insert(p1);

    for(int n = 2; n <= maxn; n++){
        for(auto p : Poly[n - 1]){
            for(auto t : p){
                for(int i = 0; i < 4; i++){
                    int nx = t.x + dx[i];
                    int ny = t.y + dy[i];
                    Cell c(nx, ny);
                    if(p.count(c) == 0) check(p, c, n);
                }
            }
        }
    }
}

int getAns(int n, int w, int h){
    int minx, miny, maxx, maxy;
    int cnt = 0;

    for(auto p : Poly[n]){
        minx = miny = inf;
        maxx = maxy = 0;
        for(auto t : p){
            minx = min(minx, t.x);
            miny = min(miny, t.y);
            maxx = max(maxx, t.x);
            maxy = max(maxy, t.y);
        }
        int lx = maxx - minx;
        int ly = maxy - miny;
        if(min(lx, ly) < min(w, h) && max(lx, ly) < max(w, h)){
            cnt++;
        }
    }

    return cnt;
}

int main(){
    #ifndef ONLINE_JUDGE
        freopen("in.txt", "r", stdin);
    #endif

    int n, w, h;

    search();

    while(cin >> n >> w >> h){
        int ans = getAns(n, w, h);
        cout << ans << endl;
    }
    return 0;
}