Kalman filter-卡尔曼滤波器

发表于 | 分类于 | | 阅读次数:

　　卡尔曼滤波理论，由卡尔曼博士在1960年访问NASA时首次提出，震惊了NASA，促成了著名的“阿波罗”计划，使人类第一次登上月球。

Rudolf_Kalman

什么是卡尔曼滤波

　　维基百科上的解释：卡尔曼滤波是一种高效率的递归滤波器，它能从一系列的不完全及包含杂讯的测量中，估计动态系统的状态。
　　简单来说就是它可以有效利用多个粗糙数据之间的关系，对多个数据进行融合。下面举个简单的例子：

例子来源Kent Zeng
　　假设我们有两个传感器，测的是同一个信号，譬如说物体的位置$(x, y, z)$。可是它们每次的读数都不太一样，即传感器的信号有波动，怎么办？
　　取平均。
　　再假设我们知道其中那个价格贵一些的传感器应该更准一些，比取平均更好的方法是：
　　取加权平均。即我们把精度更高的传感器的权值设的高一点，表示我们更相信它的测量结果。假设两个传感器的测量误差都符合正态分布，我们可以将这两个正态分布合成为一个新的正态分布。具体过程在下面的原理部分讨论，这种理解方式很重要。
　　但是如果我们只有一个传感器，但是还有一个数学模型，譬如物体的运动模型。模型可以帮我们算出一个物体的位置值，但也不是那么准。怎么办？
　　把模型算出来的值和传感器测出来的值，像两个传感器那样，取加权平均。

卡尔曼滤波原理

运动模型

　　同样我们用测量物体的位置的例子来说明。假设我们要实时的得到机器人在空间中的位置。如上面所说，我们需要一个机器人的运动模型，如果我们不知道机器人确切的运动模型，可以先简单的假定其为匀速运动模型。
　　有了运动模型之后，我们就可以通过一组状态变量$x$来描述机器人在某一时刻的状态，包括位置$p$和速度$v$。

$$
x=
\begin{bmatrix}
p \\
v \\
\end{bmatrix}
$$

　　这里的$x, p, v$都是向量，其中，$p=\begin{bmatrix} x \\ y \\ z \end{bmatrix}$，$v=\begin{bmatrix} v_x \\ v_y \\ v_z \end{bmatrix}$
　　这里我们只记录了位置和速度，但是取决于我们的模型以及我们期望获得的数据我们可以把任何数据变量放进系统状态里。
　　用运动方程来表示我们建立的匀速模型：

$$
p_k = p_{k - 1} + \Delta t \times{v_{k - 1}} \\
v_k = v_{k - 1}
$$

　　写成矩阵形式：

$$
x_k=
\begin{bmatrix}
p_k \\
v_k \\
\end{bmatrix}
=
\begin{bmatrix}
1 & \Delta t \\
0 & 1 \\
\end{bmatrix}
\begin{bmatrix}
p_{k -1} \\
v_{k - 1} \\
\end{bmatrix}
$$

　　因为$x$实际上是一个包含三个位置量和三个速度量的六维向量，所以由$x_{k - 1}$到$x_{k}$的转移矩阵可具体表示为：

$$
x_k=
\begin{bmatrix}
1 & 0 & 0 & \Delta t & 0 & 0 \\
0 & 1 & 0 & 0 & \Delta t & 0 \\
0 & 0 & 1 & 0 & 0 & \Delta t \\
0 & 0 & 0 & 1 & 0 & 0 \\
0 & 0 & 0 & 0 & 1 & 0 \\
0 & 0 & 0 & 0 & 0 & 1 \\
\end{bmatrix}
x_{k - 1}
$$

　　把转移矩阵记为$F$，则$x_k = Fx_{k - 1}$
　　卡尔曼滤波假设所有变量的值符合正态分布，那么系统各变量间的不确定度可以用协方差来表示，系统状态的协方差记为$P_k$，这是一个$6\times{6}$的对称矩阵。
　　由于我们有下面的公式：

$$
Cov(x) = \Sigma \\
Cov(Ax) = A \Sigma A^T
$$

　　所以综合上面的运动模型我们可以得到状态变量以及误差的更新公式：

$$
x_k = Fx_{k - 1} \\
P_k = FP_{k -1}F^T
$$

　　之前提到我们的模型一般不会是100%准确的，那么就会存在一个预测误差，我们把这个预测误差矩阵记为$Q$，表示预测上的高斯噪声。对误差做简单的叠加，可以得到完整的预测转换方程：

$$
x_k = Fx_{k - 1} \\
P_k = FP_{k - 1}F^T + Q
$$

　　Ps.有时我们会看到$x_k = Fx_{k - 1} + Bu_k$这种转移方程的写法，这是引入了一个可以预测的外力影响因素，表示系统当前状态并不只依靠上一个系统状态。譬如，机器人的运动受当时风速的影响，那么$u_k$就表示风速变量，$B$表示风速变量到系统状态变量的转换矩阵。

观测模型

　　我们还需要一个（或多个）传感器来提供系统状态的观测数据，通过测量值来精炼上一阶段模型的预测值。传感器所能够测得的变量由其功能决定，假设我们现在有一个传感器可以直接得到机器人的位置状态量$p$，$p=\begin{bmatrix} x & y & z \end{bmatrix}^T$。
　　注意传感器测量量的范围和单位可能与系统状态变量的范围和单位不一致，所以我们需要做如下变换：

$$
\mu = Hx_k \\
\Sigma = HP_kH^T
$$

　　其中$H$为变换矩阵，具体到我们所讨论的例子，传感器只能测得6个系统状态量中的3个，所以要做如下变换，把系统状态量变换到传感器测量空间中去：

$$
\begin{bmatrix}
x \\
y \\
z \\
\end{bmatrix}
=
\begin{bmatrix}
1 & 0 & 0 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 & 0 & 0 \\
\end{bmatrix}
\begin{bmatrix}
x \\
y \\
z \\
v_x \\
v_y \\
v_z \\
\end{bmatrix}
$$

　　传感器也有自己的精度范围，换句话说传感器的读数会收到高斯噪声的影响在某个范围内波动。我们把传感器测量值不确定性的方差记为$R$，传感器实际返回的值（即正态分布均值）记为$z_k$。

数据融合

　　现在每一时刻我们都有了两个高维的正态分布模型，一个来自模型的预测值，另一个来自传感器的测量值。我们尝试去进行数据的融合。其实非常简单，对每一个模型来说我们有了它在空间各个位置的概率密度函数，我们需要找到最大可能性的那个位置，那么我们只要将两者相乘就好了。
　　非常值得高兴的是，两个正态分布相乘，结果还是一个正态分布！于是新的正态分布的均值位置就是两模型相乘后概率密度最大的位置处。理所当然的我们就可以把它选做该时刻的机器人的位置估计值。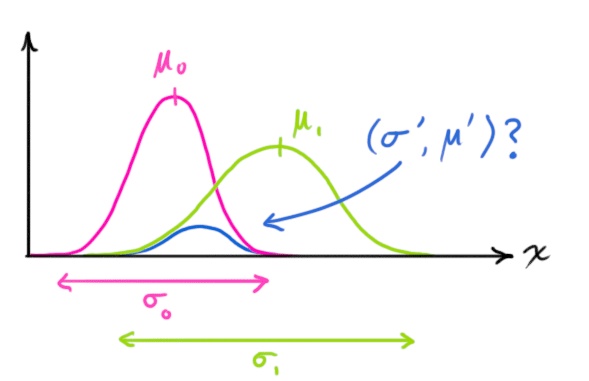
gauss

　　下面做一些简要的推导：

太懒了直接贴图，来源米开朗基罗赵

　　一维正态分布定义：

g1

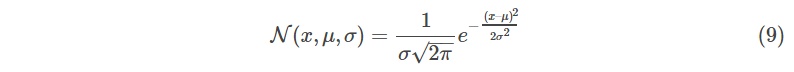
　　我们想知道两个均值、方差不同的正态分布相乘的结果：

g2

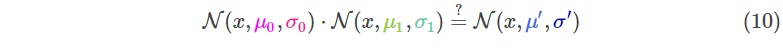
　　把公式(9)带入(10)然后做一些变换，可以得到：

g3

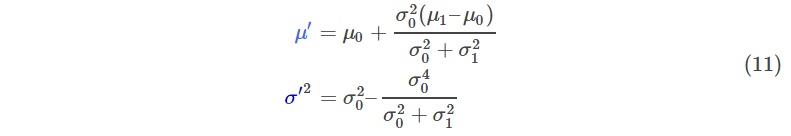
　　因式分解出一部分，表示为$k$：

g4

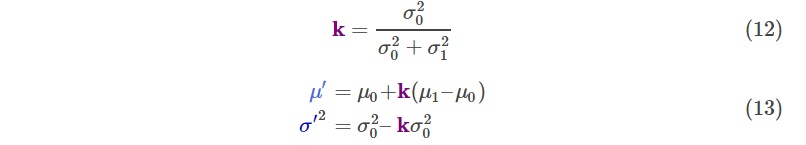
　　上面是一维的情况，扩展到高维，直接把(12)和(13)表示成矩阵形式就好了：

g5

　　现在出现的这个$K$就是那个让人很难理解的卡尔曼增益了，但是在这里这很简单，只是两个正态分布合并过程中因式分解出的一项。
　　现在我们来把(14)和(15)中的变量替换一下，替换成我们分析出的运动模型和观测模型的均值、方差，其中把运动模型变换到传感器测量空间中：

$$
(\mu_0, \Sigma_0)=(Hx_k, HP_kH^T) \\
(\mu_1, \Sigma_1)=(z_k, R)
$$

　　经过化简，我们就可以得到三个更新公式了，再加上之前的两个运动模型方程，共同组成卡尔曼滤波的五个核心公式：

$$
x_k = Fx_{k - 1} \\
P_k = FP_{k - 1}F^T + Q \\
K = P_kH^T(HP_kH^T + R)^{-1} \\
\hat{x_k} = x_k + K(z_k - Hx_k) \\
\hat{P_k} = (I - KH)P_k
$$

　　其中$\hat{x_k}$为该时刻的位置估计值，同时将作为下一次迭代的$x_{k - 1}$，$\hat{P_k}$为更新后的系统方差，将作为下一下迭代的$P_{k - 1}$

实例

　　这一部分是一个实例，具体背景是我通过双目相机追踪并还原了手指在空间中运动的一些三维轨迹点（螺旋上升轨迹），但是数据有些噪音（波动），下面是原始数据以及用卡尔曼滤波后的效果图：

origin
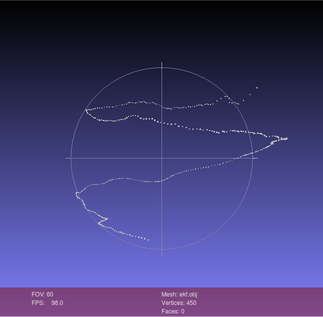
afterFilter

附上源代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
/*
 *
 * Author : Aincrad
 *
 * Date : Thu 18 Apr 18:51:49 CST 2019
 *
 */

#include <Eigen/Core>
#include <Eigen/LU>
#include <iostream>
#include <fstream>

using namespace std;
using namespace Eigen;

typedef Matrix<double, 6, 6> Matrix6d;
typedef Matrix<double, 6, 1> Vector6d;

int main(int argc, char* argv[]){
    char c;
    double x, y, z, dx, dy, dz;
    double nx, ny, nz;
    double x1, y1, z1, x2, y2, z2;

    Matrix6d F, P, Q, P_;
    Matrix<double, 3, 6> H;
    Matrix<double, 6, 3> G;
    Matrix3d R;

    ifstream fin;
    ofstream fout;
    fin.open(argv[1]);
    fout.open(argv[2]);
    fin >> c >> x1 >> y1 >> z1;
    fin >> c >> x2 >> y2  >> z2;
    fout << c << " " << x1 << " " << y1  << " " << z1 << endl;
    fout << c << " " << x2 << " " << y2  << " " << z2 << endl;
    x = x2, y = y2, z = z2;
    dx = x2 - x1, dy = y2 - y1, dz = z2 - z1;

    Vector6d X, X_;
    Vector3d Z;
    X << x , y , z , dx , dy , dz;

    F << 1, 0, 0, 1, 0, 0,
         0, 1, 0, 0, 1, 0,
         0, 0, 1, 0, 0, 1,
         0, 0, 0, 1, 0, 0,
         0, 0, 0, 0, 1, 0,
         0, 0, 0, 0, 0, 1;

    H << 1, 0, 0, 0, 0, 0,
         0, 1, 0, 0, 0, 0,
         0, 0, 1, 0, 0, 0;

    P = Matrix6d::Identity() * 1;

    Q = Matrix6d::Identity() * 1e-4;
    R = Matrix3d::Identity() * 1;

    while(fin >> c >> nx >> ny >> nz){
        Z << nx , ny , nz;

        X_ = F * X;
        P_ = F * P * F.transpose() + Q;

        G = P_ * H.transpose() * (H * P_ * H.transpose() + R).inverse();
        X = X_ + G * (Z - H * X_);
        P = (Matrix6d::Identity() - G * H) * P_;
        
        fout << "v " << X(0) << ' ' << X(1) << ' ' << X(2) << endl;
    }

    fin.close();
    fout.close();

    return 0;
}

使用cmake编译，CMakeLists.txt中的内容：

1
2
3
4
5
6
7
cmake_minimum_required(VERSION 3.5.1)
project(Ekf)

find_package(Eigen3 REQUIRED)
include_directories(${EIGEN3_INCLUDE_DIRS})

add_executable(ekf ekf.cpp)

参考链接

The Extended Kalman Filter:An Interactive Tutorial for Non-Experts
卡尔曼滤波－－从推导到应用
如何通俗并尽可能详尽解释卡尔曼滤波
理解Kalman滤波的使用

　　这些文章在我学习卡尔曼滤波的过程中给予了我很大的帮助，感谢各位博主。其中第三个链接为知乎的回答，我主要参考了其中的[Kent Zeng]用户、[太空精酿]用户以及[米开朗基罗赵]用户的回答。

总结

　　卡尔曼老爷子实在是太强了Orz。