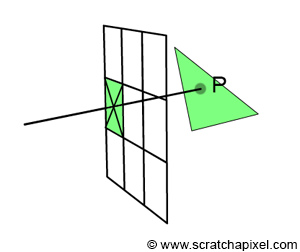
如何确定投影区域内每个像素对应的空间物体上一点的深度是本节主要讨论的内容。
Z-Buffer
在光栅化算法总述里我们提到当有多个三角形相互重叠时,它们之上的某些点可能会投影到同一个像素位置,我们要通过z-buffer方法来确定这些点的深度大小关系,从而决定像素显示哪一点的颜色。
z-buffer是一个二维矩阵,矩阵元素初始化为一个较大的值,当遍历三角面片进行投影时不断更新元素值,用来记录每个像素对应的距离相机最近的空间物体上一点的深度。
深度插值
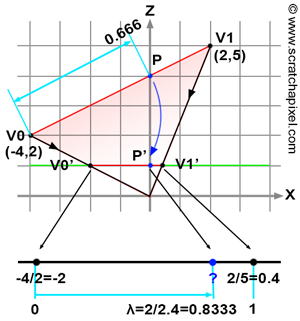
关于如何求解每个像素对应的空间深度值,首先想到的可能是借助上一节提到的重心坐标插值的方法。但是由于投影后的比例变化(Figure 1),我们不能直接把投影平面上三角形的面积比作为空间三角形的面积比来得到重心坐标。
我们的目标是由投影平面上三角形的重心坐标来推出空间三角形上对应一点的深度值。在透视投影部分我们得到了投影坐标:
$$
\begin{align}
&P_{screen}.x = \cfrac{near * P_{camera}.x}{-P_{camera}.z} \\
&P_{screen}.y = \cfrac{near * P_{camera}.y}{-P_{camera}.z} \\
&P_{screen}.z = -P_{camera}.z
\end{align}
$$
投影之后我们仍然保留空间点的z坐标,利用它们还原计算空间三角形上任一点的深度值。
如图(Figure 2),为了简化问题,我们仍只考虑一条在相机空间中的线段,它的两个端点的坐标分别为 $P_0(X_0, Z_0)$ 和 $P_1(X_1, Z_1)$ ,两端点在成像平面上的投影坐标分别为 $S_0$ 和 $S_1$。$S$ 是投影线段上的一点,其分割线段的比例是 $(1 - q):q$ (即重心坐标),$P$ 是 $S$ 对应的原线段上的点,其重心坐标为 $(1-t):t$。
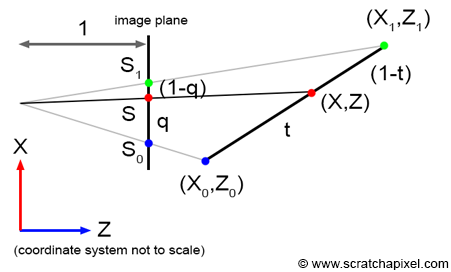
我们可以得到如下关系式:
$$
P = P_0 * (1 - t) + P_1 * t
S = S_0 * (1 - q) + S_1 * q
$$
也可以写做如下形式:
$$
P = P_0 + t * (P_1 - P_0)
S = S_0 + q * (S_1 - S_0)
$$
S是一维的坐标点,我们下面用它来同时指代自己的坐标值
于是我们可以插值得到 $P$ 和 $S$ 的坐标(Equation 1):
$$
\begin{align}
&(X, Z)=(X_0 + t * (X_1 - X_0), \quad Z_0 + t * (Z_1 - Z0)) \\
& \\
&S = S_0 + q * (S_1 - S_0)
\end{align}
$$
由相似三角形的比例关系我们可以得到(假设近平面距离near为一个单位长度):
$$
\cfrac{S}{X} = \cfrac{1}{Z}
$$
即:
$$
Z = \cfrac{X}{S}
$$
把(Equation 1)带入上式得(Equation 2):
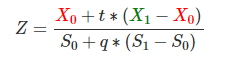
类似的我们还有:
$$
S_0 = \cfrac{X_0}{Z_0} \\
S_1 = \cfrac{X_1}{Z_1}
$$
因此(Equation 3):
$$
X_0 = S_0 * Z_0 \\
\\
X_1 = S_1 * Z_1
$$
把(Equation 3)带入到(Equation 2)中得到(Equation 4):
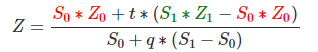
由(Equation 1)中我们知道(Equation 5):
$$
Z = Z_0 + t * (Z_1 - Z0)
$$
带入(Equation 4)中得(Equation 6):
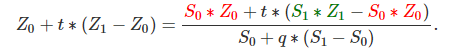
化简(Equation 5)得:
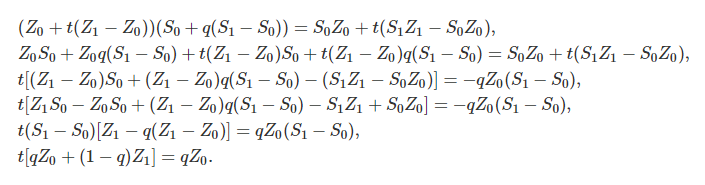
我们现在可以把变量 $t$ 替换掉了:
$$
t = \cfrac{qZ_0}{qZ_0 + (1 - q)Z_1}
$$
带入(Equation 5)中得:

进而我们就可以得到:
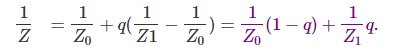
至此我们就得到了如何通过投影平面上一点的重心坐标得到其对应空间点的深度的公式。