
画家用透视投影的方法作画,以获得接近真实三维物体的视觉效果。
透视投影
透视投影是三维投影的一种,是将三维空间中的点映射到二维平面上的方法。由于目前绝大多数图形数据的显示方式仍是二维的,因此三维投影的在计算机图形学等方面应用广泛。
投影原理
透视投影符合人眼成像的特点,以人眼作为视点,在视网膜上的图像就是空间物体投影的结果。
如图(Figure 1),点 $P$ 为空间中的一点,$P^\prime$ 为其投影在成像平面上的点,$A$ 为视点。
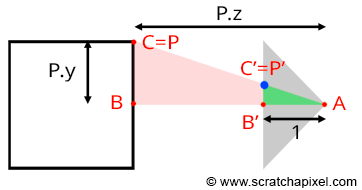
由 $\Delta ABC$ 和 $\Delta AB^\prime C^\prime$ 相似可以得到:
$$
\cfrac{BC}{AB}=\cfrac{B^\prime C^\prime}{AB^\prime},即 \cfrac{P.y}{P.z}=\cfrac{P^\prime.y}{near}
$$
其中near为视点到成像平面的距离。
$$P^\prime.y=\cfrac{near * P.y}{P.z}$$
同理可得,
$$P^\prime.x=\cfrac{near * P.x}{P.z}$$
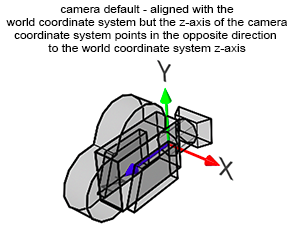
由于默认情况下相机指向z轴的负半轴(Figure 2),所以实际上要对相机坐标系下的z轴坐标取反。
$$
P_{screen}.x = \cfrac{near * P_{camera}.x}{-P_{camera}.z} \\
P_{screen}.y = \cfrac{near * P_{camera}.y}{-P_{camera}.z}
$$
假设图片的尺寸为 $W * H$,那么投影后的坐标与该点可见性的关系如下:
$$
visible=
\begin{cases}
yes & |P_{screen}.x| <= \cfrac{W}{2} \quad \text{or} \quad |P_{screen}.y| <= \cfrac{H}{2} \\
no & \text{otherwise}
\end{cases}
$$
坐标系变换
我们的目标是获得投影点的像素坐标,所以要对坐标系进行变换,由成像平面坐标系变为光栅坐标系。
相机成像平面上一点 $P_{screen}$ (Figure 3)
先将其转换为 $NDC$ 坐标系下(Figure 4),范围为 $[0, 1]$
$$
P_{normalized}.x=\cfrac{P_{screen}.x + W/2}{W} \\
P_{normalized}.y=\cfrac{P_{screen}.y + H/2}{H}
$$
最后转换为光栅化坐标(Figure 5)
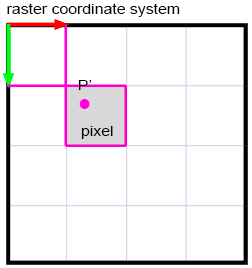
$$
P_{raster}.x=P_{normalized}.x * pixelWidth \\
P_{raster}.y=(1-P_{normalized}.y) * pixelHeight
$$
注意区分 $W$ 和 $pixelWidth$,W指的是图片的物理尺寸,以 m 或 mm 等为单位,pixelWidth指的是图片的横向像素的个数。
由此可得相机坐标系到光栅坐标系的转换公式:
$$
P_{raster}.x=(1 + \cfrac{near * P_{camera}.x}{-W * P_{camera}.z})* 0.5 * pixelWidth \\
P_{raster}.y=(1 - \cfrac{near * P_{camera}.y}{-W * P_{camera}.z}) * 0.5 * pixelHeight
$$
拓展
上面提到的 $NDC$ 坐标范围为 $[0, 1]$,实际上在GPU的实现中, $NDC$ 坐标范围为 $[-1, 1]$。另外讨论更一般的情况,假设成像平面坐标系的 $x$ 坐标范围为 $[l, r]$,$y$ 坐标范围为 $[b, t]$。
此时由成像平面坐标系到 $NDC$ 坐标系的映射关系可以通过以下方式求解,先考虑 $x$:
由 $l<=x<=r$,可得 $0<=x-l<=r-l$,各项同时除以 $(r-l)$:
$$
0 <= \cfrac{x-l}{r-l} <= 1
$$
公式各项同时乘以 $2$ 再减去 $1$:
$$
-1 <= 2 * \cfrac{x-l}{r-l} - 1 <= 1
$$
化简得:
$$
-1 <= \cfrac{2x}{r-l}-\cfrac{r+l}{r-l} <= 1,即 \quad P_{normalized}.x = \cfrac{2*P_{screen}.x}{r-l}-\cfrac{r+l}{r-l}
$$
同理可得:
$$
-1 <= \cfrac{2y}{t-b}-\cfrac{t+b}{t-b} <= 1,即 \quad P_{normalized}.y = \cfrac{2*P_{screen}.y}{t-b}-\cfrac{t+b}{t-b}
$$
参考链接
Scratchpixel-Mathematics of Computing the 2D Coordinates of a 3D Point
Scratchpixel-The Projection Stage