光栅化渲染(3)-光栅化

发表于 | 分类于 ， | | 阅读次数:

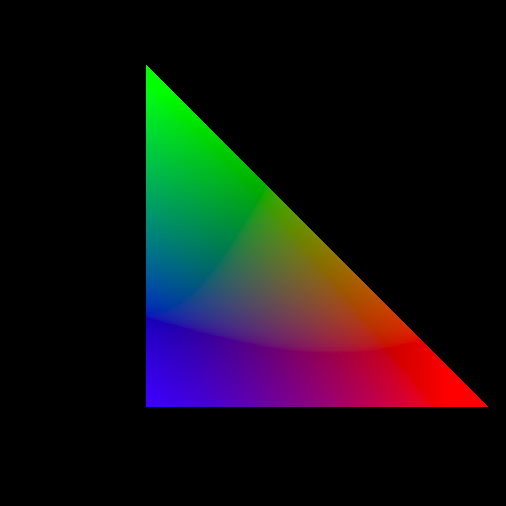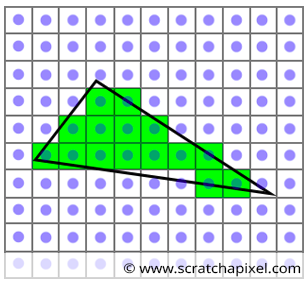
rasterization

　　通过检测图像中的像素是否处在投影后的三角形中，来赋予像素相应的颜色的属性，是光栅化算法的主要思路。

光栅化

　　为了实现一个简易的光栅化效果（在屏幕上画出一个三角形），我们需要解决两个问题：

  • 首先要找到所有落在三角形投影范围内的像素。
  • 为以上位置的像素赋予相应的颜色。

　　Edge Function可以很好的解决第一个问题，快速判断一个像素是否在三角投影区域内。第二个问题也被成为shading（着色）。

The Edge Function

　　Edge Function 由 Juan Pineda 在 1988 年发表的一篇名为 A parallel Algorithm for Polygon Rasterization 的论文中提出。
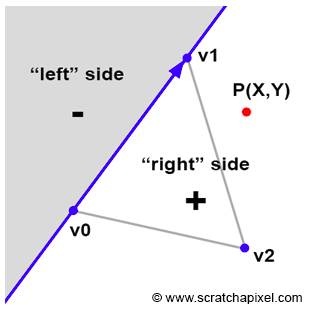
　　三角形的一边可以看作是分割二维平面的一条线(Figure 1)，Pineda 的方法的主要思路是找到一个方程，用它来测试任一给定点 $P(x, y)$ 处于分割线的哪一侧：

  • 当点 $P$ 位于分割线的左侧时，方程返回一个负值。
  • 当点 $P$ 位于分割线的右侧时，方程返回一个正值。
  • 当点 $P$ 正好位于分割线之上时，方程返回0。

figure 1

Figure 1

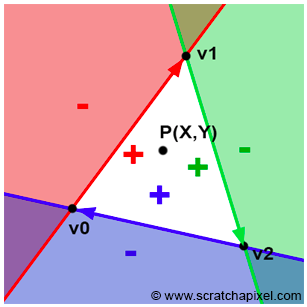
　　于是我们可以发现分别以三角形的三条边作为分割线的话，若某一点 $P(x, y)$ 经过Edge Function测试全为正，即点 $P(x, y)$ 全部位于三角形三边的右侧，那么就可以确定这一点位于三角形内部。
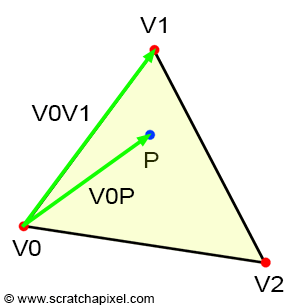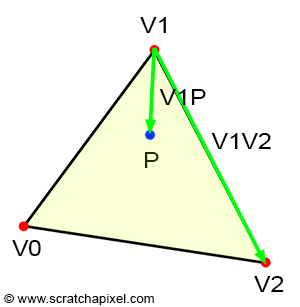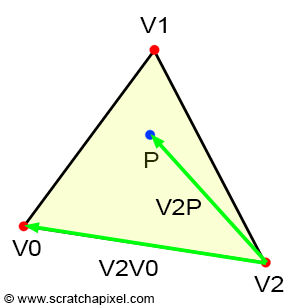
　　需要注意三角形三边的方向，按照顺时针定义，即三边分别为 v0->v1，v1->v2，v2->v0。

figure 2

Figure 2

　　了解了Edge Function的设计思路，下面给出它的公式（关于边$V0->V1$）：

$$
E_{01}(P)=(P.x-V0.x)*(V1.y-V0.y)-(P.y-V0.y)*(V1.x-V0.x)
$$

　　事实上这也是向量 $(P-v0)$ 和 $(V1-V0)$ 叉积的大小值，可以用行列式矩阵表示：

$$
\left[
\begin{matrix}
P.x-V0.x & V1.x-V0.x \\
P.y-V0.y & V1.y-V0.y
\end{matrix}
\right]
$$

　　不难理解，Edge Function的结果的正负性和向量叉积值的正负性是一致的。
　　所以判断某一像素是否位于投影三角形内，只需检测由像素中心坐标 $P(x, y)$ 和三角形三边所定义的三个Edge Function的正负性。

$$
E_{01}(P)=(P.x-V0.x)*(V1.y-V0.y)-(P.y-V0.y)*(V1.x-V0.x) \\
E_{12}(P)=(P.x-V1.x)*(V2.y-V1.y)-(P.y-V1.y)*(V2.x-V1.x) \\
E_{20}(P)=(P.x-V2.x)*(V0.y-V2.y)-(P.y-V2.y)*(V0.x-V2.x)
$$

figure 3

Figure 3

重心坐标

　　通常我们只能对三角形的三个顶点定义颜色等属性，那么如何确定三角形内部任意一点的颜色？(Figure 4)

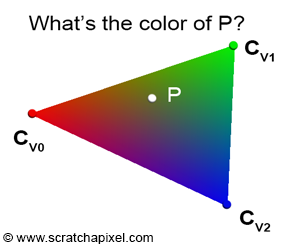
figure 4

Figure 4

　　假设 $P=\lambda_{0} * V0 + \lambda_{1} * V1 + \lambda_{2} * V2$，且满足 $\lambda_{0} + \lambda_{1} + \lambda_{2} = 1$ 那么 $(\lambda_{0},\lambda_{1},\lambda_{2})$ 就是 $P$ 的重心坐标。它可以表示位于三角形内部（及边界）上的任意一点。
　　于是我们可以借助重心坐标来对三角形内任意一点进行插值，以获得其颜色 $C_P$ 等其它由顶点定义的属性：

$$
C_P=\lambda_{0} * C_{V0} + \lambda_{1} * C_{V1} + \lambda_{2} * C_{V2}
$$

如何获得任意一点的重心坐标

　　在三角形情形中，重心坐标也叫面积坐标，因为 $P$ 点关于 $\Delta ABC$ 的重心坐标和 $\Delta PBC, \Delta PCA, \Delta PAB$ 的面积成比例。证明如下。
　　如图(Figure 4)，设 $\Delta ABC$ 三个顶点和原点构成的向量分别为 $pmb{\vec{a}}, \pmb{\vec{b}}, \pmb{\vec{c}}$，$P$ 点和原点构成的向量为 $\pmb{\vec{p}}$。$\Delta PBC, \Delta PCA, \Delta PAB$ 面积之比为 $\lambda_{0}:\lambda_{1}:\lambda_{2}$，且 $\lambda_{0} + \lambda_{1} + \lambda_{2}=1$，设射线 $AP$ 与 $BC$ 交于点 $D$，点 $D$ 和原点构成的向量为 $\pmb{\vec{d}}$，

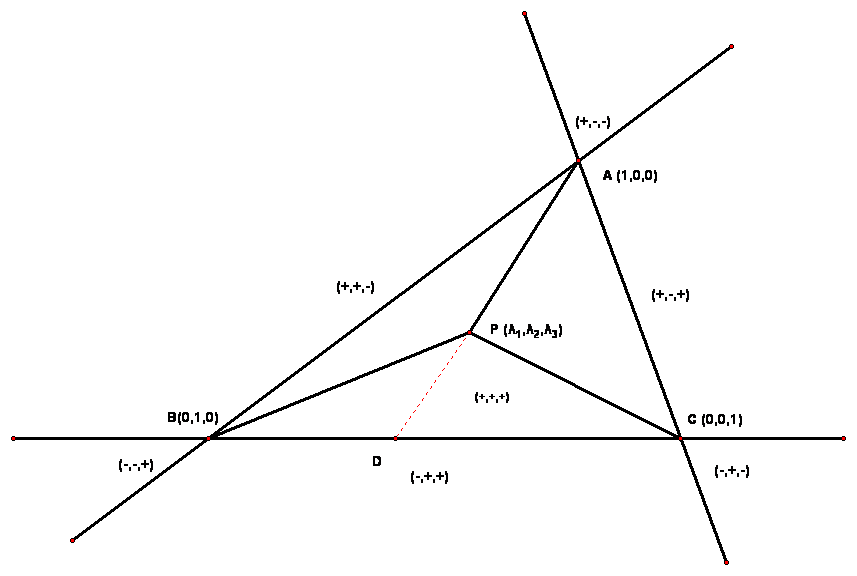
figure 5

Figure 5

　　则：

$$
BD:DC=\lambda_{2}:\lambda_{1}, 从而\quad \pmb{\vec{d}}=\cfrac{\lambda_{1}\pmb{\vec{b}}+\lambda_{2}\pmb{\vec{c}}}{\lambda_{1}+\lambda_{2}} \\
AP:PD=(\lambda_{1}+\lambda_{2}):\lambda_{0}, 故\quad \pmb{\vec{p}}=\cfrac{(\lambda_{1}+\lambda_{2})\pmb{\vec{d}}+\lambda_{0}\pmb{\vec{a}}}{\lambda_{0}+\lambda_{1}+\lambda_{2}} \\
\pmb{\vec{p}}=\lambda_{0}\pmb{\vec{a}}+\lambda_{1}\pmb{\vec{b}}+\lambda_{2}\pmb{\vec{c}}
$$

　　而 $\Delta PBC, \Delta PCA, \Delta PAB$ 的面积又正好等于 $P$ 点和 $\Delta ABC$ 顶点构成的向量与 $\Delta ABC$ 三边构成的向量的叉积的值的一半。
　　叉积值已通过 Edge Function 得到，所以重心坐标：

$$
\lambda_{0}=\cfrac{Area(V1,V2,P)}{Area(V0,V1,V2)}=\cfrac{E_{12}(P)/2}{E_{12}(V0)/2}=\cfrac{E_{12}(P)}{E_{12}(V0)} \\
\lambda_{1}=\cfrac{Area(V2,V0,P)}{Area(V0,V1,V2)}=\cfrac{E_{20}(P)/2}{E_{20}(V1)/2}=\cfrac{E_{20}(P)}{E_{20}(V1)} \\
\lambda_{2}=\cfrac{Area(V0,V1,P)}{Area(V0,V1,V2)}=\cfrac{E_{01}(P)/2}{E_{01}(V2)/2}=\cfrac{E_{01}(P)}{E_{01}(V2)}
$$

计算优化

$$
lambda_{0} + lambda_{1} + lambda_{2} = 1 \\
P = lambda_{0} * V0 + lambda_{1} * V1 + lambda_{2} * V2
$$

　　两公式联立消去 $\lambda_{0}$ 得：

$$
P=V0 + lambda_{1} * (V1-V0) + lambda_{2} * (V2-V0)
$$

　　$V1-V0$ 和 $V2-V0$ 可以提前计算出来，这样就把计算由三次乘法和两次加法简化到了两次乘法和两次加法。GPU采用了这种优化策略。

拓展

　　在某些特殊情况下，一个像素可能同时落在两个投影三角形区域内，Figure 6 中的红色像素点显示了这种情况。

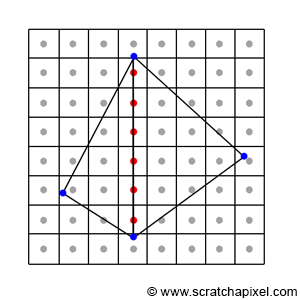
figure 6

Figure 6

　　top-left rule (Figure 7) 可以用来避免这种重复光栅化三角形边界像素的情况。

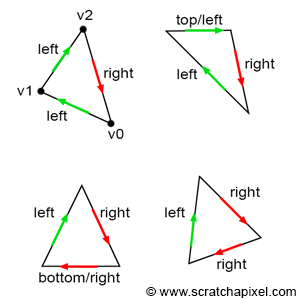
figure 7

Figure 7

　　由图可知：

  • top edge 指的是满足向量 $V[(x+1)%3] - V[x], x=0,1,2$ 的 $y$ 坐标等于 $0$，且 $x$ 坐标大于 $0$ 的边。
  • left edge 指的是满足向量　$V[(x+1)%3]-V[x], x=0,1,2$ 的 $y$ 坐标大于 $0$ 的边。

　　需要特别注意的是，本节都是建立在三角形三边按顺时针方向定义的前提下讨论的。

实例

　　给定光栅化坐标系下的三角形的三个顶点以及顶点的颜色，渲染出这个三角形。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
#include <iostream>
#include <fstream>
#include <cstring>

struct Vec2{
    float x, y;
    Vec2(float x = 0.0, float y = 0.0): x(x), y(y){}
};

struct Vec3{
    float x, y, z;
    Vec3(float x = 0.0, float y = 0.0, float z = 0.0): x(x), y(y), z(z){}
};

struct Rgb{
    unsigned char r, g, b;
    Rgb(unsigned char r = 0, unsigned char g = 0, unsigned char b = 0): r(r), g(g), b(b){}
};

float edgeFunction(Vec2 &a, Vec2 &b, Vec2 &c){
    return (c.x - a.x)*(b.y - a.y) - (c.y - a.y)*(b.x - a.x);
}

bool top_left(const Vec2 &v){
    if((v.y == 0 && v.x > 0) || v.y > 0) return true;
    else return false;
}

int main(){
    Vec2 v0(491.407, 411.407); 
    Vec2 v1(148.593, 68.5928); 
    Vec2 v2(148.593, 411.407); 
    Vec3 c0(1, 0, 0); 
    Vec3 c1(0, 1, 0); 
    Vec3 c2(0, 0, 1);

    const uint32_t w = 512;
    const uint32_t h = 512;

    Rgb framebuffer[w][h];
    memset(framebuffer, 0, sizeof(framebuffer));

    float area = edgeFunction(v0, v1, v2);

    for(uint32_t j = 0; j < h; j++){
        for(uint32_t i = 0; i < w; i++){
            Vec2 p(i + 0.5, j + 0.5);
            float w0 = edgeFunction(v1, v2, p);
            float w1 = edgeFunction(v2, v0, p);
            float w2 = edgeFunction(v0, v1, p);

            if(w0 >= 0 && w1 >= 0 && w2 >= 0){
                //top-left judge
                if(w0 == 0 && !top_left(Vec2(v2.x - v1.x, v2.y - v1.y))) continue;
                if(w1 == 0 && !top_left(Vec2(v0.x - v2.x, v0.y - v2.y))) continue;
                if(w2 == 0 && !top_left(Vec2(v1.x - v0.x, v1.y - v0.y))) continue;

                w0 /= area;
                w1 /= area;
                w2 /= area;
                float r = w0 * c0.x + w1 * c1.x + w2 * c2.x;
                float g = w0 * c0.y + w1 * c1.y + w2 * c2.y;
                float b = w0 * c0.z + w1 * c1.z + w2 * c2.z;
                framebuffer[j][i].r = (unsigned char)(r * 255);
                framebuffer[j][i].g = (unsigned char)(g * 255);
                framebuffer[j][i].b = (unsigned char)(b * 255);
            }
        }
    }

    std::ofstream ofs;
    ofs.open("./raster2d.ppm");
       ofs << "P6\n" << w << " " << h << "\n255\n";
    ofs.write((char *)framebuffer, sizeof(framebuffer));
    ofs.close(); 

    return 0;
}

结果

result

result

参考链接

Scratchapixel-The Rasterization Stage
维基百科-重心坐标